In which I discuss the hexagon, natures greatest shape, and muse about a paper on the history of hexagonal city planning.
The humble honeybee builds a happy hive out of the hexagon, and why can’t we do the same?
While I will refute the claim made by CPG Grey (2020) that the hexagon is the strongest shape (that goes to the terrific triangle (Hathy, 2023)) I am not an engineer, and this essay is not interested in structural strength. Considering surfaces, a mathematician like myself is only concerned with area and perimeter.
Here a hexagon has numerous advantages, particularly pertinent being a perimeter-to-surface area ratio. Proven as recently as 1999, hexagons outperform all other shapes for tiling a given area, including the staple square and any unconventional tiling configurations.
Sparing you the full formal proof (Hales, 1999), the reasoning is as follows:
- The closer a shape is to a circle, the better its perimeter-to-area ratio.
- Using more than one type of shape is inefficient because any gain from one shape is offset by losses from another (e.g., octagon and square tiling).
- Shapes with irregular sides are less efficient: any gain from bulging one side closer to a circle is lost by the neighboring shape bulging inward.
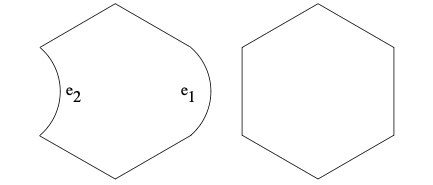
Figure 1. Bulging Hexagon. Hales (1999). Gain in e1 is loss in e2
Therefore, we want a regular shape (a shape with all angles and sides equal) that can tile with itself. Only shapes with six or fewer sides can do this (triangles, squares, and hexagons). Among these, the hexagon is the closest to a circle, making it the optimal tiling shape.
The reduction in building material required to border an internal space is where a hexagon truely shines. Minimizing material is often a worthy goal both economically and environmentally, and we can optimize with a hexagon when segmenting spaces. Should you wish to mark a domain with paving stones, or surround a section in road, you can get the most area for your given material with a hexagon. The honeybee knows this well, optimizing its hive (and eyes) via this principal of material minimization, choosing the efficient hexagon.
You may be wondering, “but surely a circle is better” and in some contexts I’ll agree. The common circle can come out ahead when only one interior is desired. Having only a single eye in each socket, I wouldn’t give up my circle anytime soon. However, should your circular yard line up with your neighbors the substantial space lost when tessellating with a circle leaves a lot to be desired. The same concern inhibits all other shapes, dodecagon, pentagons, and other fun designs. Here the honeybee too chooses well, with its compound eyes consisting of hypnotic hexagons.
The hassle-free hexagon has also been heartily adopted by the gaming community. I will be the first to admit that hexagonal battle maps are vastly superior, eliminating the need for complicated rules when moving diagonally compared to the suboptimal square. Sid Meir’s team understood this well, honing gameplay with hexagonal grids in Civilization 5 and 6. Beyond that, two-sided D&D maps allow me to choose a grid type at will. Where possible I choose the hexagon heralding in heroic gameplay. However, my design skills have not harmonized with my grid — I build many of my D&D props out of lego, which allows for 3×3 studs to neatly fit in a 1” square. Such simplicity in building steals away my gameplay from hexagons and often results in my group playing on square grids despite the suboptimal movement rules it produces.
Sometimes it’s not diagonals but intersections which are the problem, and here I particularly like hexagonal road design. It minimizes the amount of concrete needed to construct major roadways by an estimated 10% (Ben-Joseph and Gordon, 2000). It also minimizes collision points, from a typical grid’s 16 to a nice clean 3, and increases the line of sight on incoming traffic. This should greatly reduce the severity and quantity of traffic collision. It’s important to ensure hexagon blocks stay hexagonal here, otherwise 6 branch crossways can be produced when triangles get involved producing intersections with even more collision points than the traditional square (Ben-Joseph and Gordon, 2000).
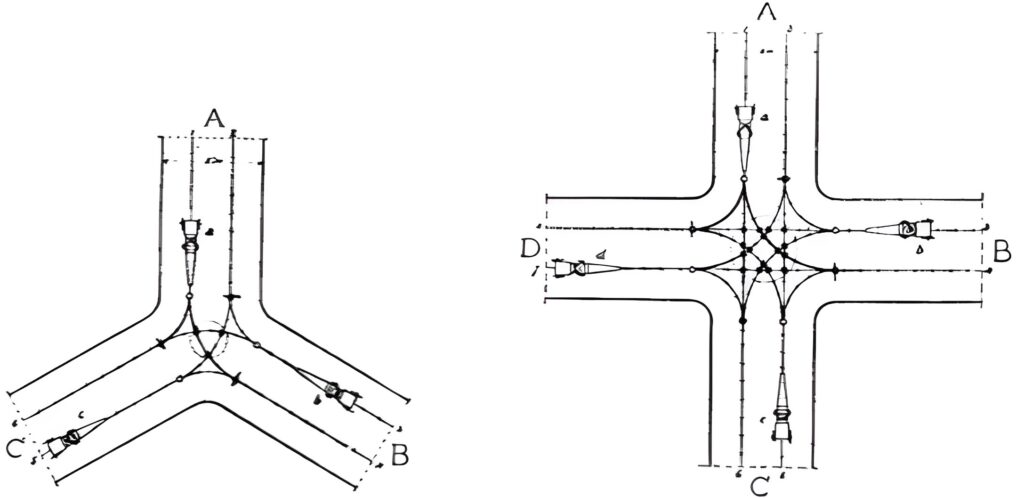
Figure 2. Three Branch Crossway (Left) with 3 collision points. Four Branch Crossway (right) with 16 collision points.
Triggs (1909), as in Ben-Joseph and Gordon (2000)
Indeed, hexagonal neighborhoods were considered as alternatives to the suburb for quite a while. Through the early 20th century planners considered many combinations of shapes to design cities, and the hexagon rose in popularity in theoretical circles as cities grew haphazardly and organically without much direction or oversight (Ben-Joseph and Gordon, 2000).
This is not to say there are no holes in this hexagonal hypothesis. My mother’s immediate mention was travel times, since square grids seem to provide travelling efficiency over hexagons. As intuitive as the supremacy of squares for speed may seem, I will remind the reader that like many things traffic it is not cut and dry. Time through intersections and travelling at diagonals (which many trips are) greatly reduces the travel speed advantage of square grids. This fact, widely known by city planners, inspires diagonal roadways, bypasses, and ring-roads. To fully compare these travel times a traffic simulation would be required – if the fancy strikes I may produce such a show, and I am also open to any analysis you, dear reader, send me.
So while waiting on evidence of travel times, should I build with hexagons? Unfortunately, our hexagon hypothesis would require more analysis than simple poetry, as there are some arguments against.
Unfortunately, some analysts who likely “fudged the numbers” (Ben-Joseph and Gordon, 2000) showed that the marginal economic advantage of hexagons was not worth the complexity, which mightily convinced the design community at the time. Regulations were passed promoting the suburb, and no hexagonal cities have been built. “Perhaps [the analysts against hexagons] were right, but we cannot be sure, since there is no hexagonal subdivision to study.” (Ben-Joseph and Gordon, 2000). Beyond this, personal tastes doomed hexagons from the start, as American homebuyers and builders did not like the triangular wedge shaped properties caused by hexagonal corners.
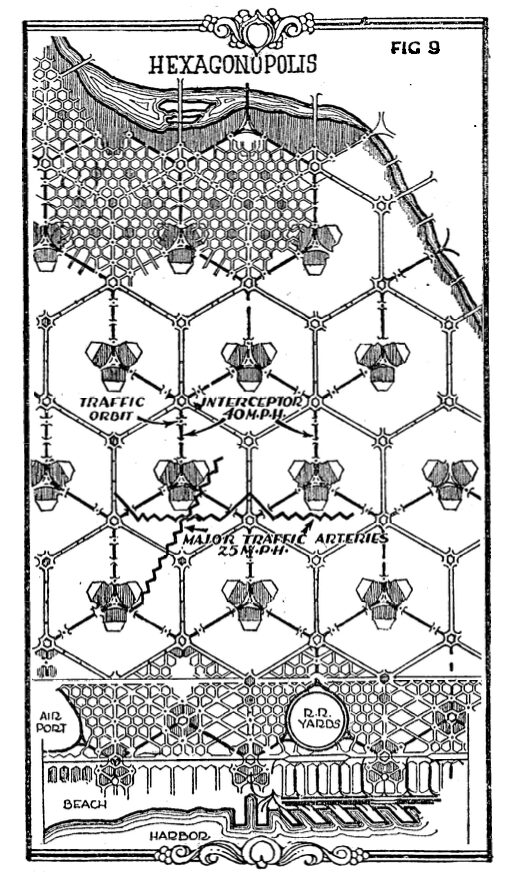
Figure 3. Hexagonopolis, Noulan Cauchon, 1927, as in Ben-Joseph and Gordon (2000).
Is an adoption of a hypothetical hexagon city plan a practical possibility? Stranger project have been started. While I certainly would not propose shifting the grids in an existing city (bulldozing housing for new roads is not my idea of a good time) building new cities from scratch is trendy these days. As we construct these new habitats for humans, we can try new ways of living, and if our consideration is geometric aesthetic, I sincerely ask we try out the bestagon, the hexagon, instead of a something completely impractical like “The Line” (Something, 2022).
References
Something, Adam. “NEOM Is The Parody Of The Future.” Youtube video, August 24, 2022 https://youtu.be/vyWaax07_ks?si=ezZstRCf1q45tPW2
Ben-Joseph, Eran and David Gordon. “Hexagonal Planning in Theory and Practice”. Journal of Urban Design, Vol. 5, No. 3 237 – 265. 2000 https://web.mit.edu/ebj/www/Hexagonal.pdf
Grey, CPG. “Hexagons are the Bestagons.” Youtube Video, November 3, 2020. https://www.youtube.com/watch?v=thOifuHs6eY
Hathy, Con. “Hexagons Are NotSoGreatAgons.” Youtube Video, June 12, 2023. https://youtu.be/4zWDLKWmBnE?si=nBefz4eBBiYm02Zz
Hales, Thomas. “The Honeycomb Conjecture”. Transactions of the American Mathematical Society, May 1, 1999. https://arxiv.org/pdf/math/9906042
Also, thanks to Frank Morgan, whose blog showed up when I was trying to find the name of the honeycomb conjecture. https://maa.org/frank-morgans-math-chat-hales-proves-hexagonal-honeycomb-conjecture
Leave a Reply